Thursday, 29 March 2007
Intepreting Yield Curves
http://fixedincome.fidelity.com/fi/FIHistoricalYield?refpr=obrfi14
The greatest shortcoming of the human race is our inability to understand the exponential function
Well, you say, what's the exponential function?
Well I gave the students this data, (shows overhead) these cam from a blue cross, blue shield ad, the add appeared in Newsweek magazine and gave these figures to show the cost escalation of gall bladder surgery in the year since 1950, when that surges cost $361. I said make a semi logarithmic plot, let's see what's happening. The students found the first four points lined up on a straight line whose slope indicated inflation of about 6% per year, but the fourth, fifth and sixth where on a steeper line almost 10% inflation per year. Well, then I said to the students, run that steeper line on out to the year 2000, lets get an idea of what a gall bladder operation might cost, 2000 was four years ago, the answer is $25,000. The lesson there was awfully clear. If you're thinking about gall bladder surgery do it now. (audience laughter)
Now in the ongoing controversy over growth in Bolder, someone wrote to the newspaper some years ago and said look, there's no problem with population growth in Boulder, because the writer said, we have fifteen times as much open space as we've already used. So let me ask you what time was it in Boulder when the open space was fifteen times the amount of space we had already used? And the answer is, it was four minutes before 12 in Boulder valley. Well suppose that at 2 minutes before 12, some of the bacterium realised they were running out of space, so they launch a great search for new bottles. They searched offshore and on the outer continental shelf and the overthrust belt and the Artic, and they find three new bottles. Now that's an incredible discovery, that's three times the total amount of resource they ever new about before, they now have four bottles, before their discovery they had one. Now surely this will give them a sustainable society, wont' it?
Now here is another look at world oil production, but this is per capita. This is litres per person each day. There is two litres, a litre is about a quart, and so two litres is about ½ gallon. The upper curve assumes there was no growth in the world population since 1920, that it stayed fluid at 1.8 billion. This then is just a copy of that earlier curve. The lower curve uses the actual population of the world and what you find is that with a growing world population this curve is pulled down more and more as you go farther to the right. And notice that peak is at about 2.2 litres per person a day in the 1970's. It is now down to about 1.7 litres a person a day, so we can say that on any day any one of us uses more than 1.7 litres of petroleum directly or indirectly, we're using more than our share. Just think about what that means.
Monday, 26 March 2007
1) Housing: Up, up, and away...
By many measures, but not all, the cost of buying a house in the UK is more expensive than ever before. House prices are also similarly high across many international markets.
Real (Inflation Adjusted) House Prices
Adjusting for inflation, “real” UK house prices are at an all time historic high. They are simply more expensive than ever before.

Price vs. Earnings ratio
The high real price of housing is reflected in the house price - earnings ratio. Traditionally this is one of the key housing measures, indicating how much earnings have kept pace with house prices. In the UK this metric once averaged within the 3-4x range, with notable spikes associated with housing boom-busts of the 1970s and late 1980s. Today this ratio is at an all time high, some 20% above the peak rates seen before. This has prompted some commentators to predict another bust.

An alternative way to measure the relative price of housing is to look at the price vs. rents ratio. This simply measures if rents are keeping track with house prices. It’s also broadly comparable to the p/e (price/earnings) ratio commonly used to measure the value of shares. Again, by this measure property in the UK this is at an historic high, with the ratio currently 50% above the long-term average, and even higher than spikes associated with the bubble markets of the 1970s and 1980s.

Source: The Economist
“Affordability”
However, both of the above measures use the actual price of the property as a yard stick to measure against. Many commentators today argue that this is misleading because property is often purchased using debt and thus it is the cost of servicing the debt that is the key measure, not the headline cost of the property nor the amount of the debt itself.

This lower “affordability” measure is driven by the low interest rate/low inflation environment that has characterised the globalised economy of the early 21st century. Low interest rates mean that for a given debt early payments are more affordable.

Unfortunately, the “affordability” description is also somewhat misleading as it does not take account of the low inflation environment that enables the low interest rates. “Affordability” as often discussed in the press is only really a measure of first year cash flow affordability and takes no account of payments in later years, nor the total cost of servicing the home loan.
Inflation has many faces. Whilst commonly viewed as public-enemy-number-one, it can actually be a friend to those in debt. If inflation is running high, interest rates and thus the cost of borrowing is generally higher too, so paying the mortgage hurts in the early years, but inflation driven wages rise rapidly and the mortgage payments quickly become much easier.

Source: Andrew Farlow
This was most typical experienced by those that bought houses during the oil shocks and stagflation of the 1970s. High inflation, and thus high interest rates, meant that many home buyers of that period will remember that they had to make significant sacrifices and experienced very tight finances for the first few years of their mortgage. However, this burden eased rapidly and they were quickly able to trade up or enjoy more spare money. It is here that the concept of a housing ladder was born.
In contrast, in a low inflation environment this “free” erosion of mortgage debt does not take place so rapidly. Low inflation lets debts linger longer. While initial payments might be cheaper than before they also stay higher for longer, and in later years the mortgage payer will pay a greater percentage of their salary than they would have done in a high inflation environment.
This has implications for the longer term.
The peak of the late 1980s boom was in 1989 and 1990. At that time UK interest rates were between 13% and 14%. It was within this context that the all-time record first year mortgage payments were eating up 60% of take home salary. However, at the same time inflation was running at over 10%. This meant that even if everything had stayed the same throughout the early 1990s it would have been approximately 10% easier to make the payments for each subsequent year of the mortgage, as earnings approximately track inflation. Thus it would have taken just over three years of a mortgage for the payments to drop from their record 60% to the 2005 rate of just over 40%, even without a change in interest rates. This is much more rapid than today, where we have inflation at circa 4% (RPI is more comparable to the inflation quoted in the 1990s than the modern CPI). As it was there was a housing bust and a recession anyway and interest rates dropped rapidly to ~6% by 1993. With this double combination of dropping interest rates and high inflation the difficulty in making mortgage payments decreased rapidly, becoming easier than the 2005 rate by 1992.
Thus, whilst the first year affordability of UK property is not yet at an historic high, the lack of inflation means the debt lingers longer. If interest rates and inflation remain broadly at current levels then the “crossover” point at which payments will become higher for today’s borrowers than even those that bought at the top of the late 1980s boom is somewhere in the 3rd year of the mortgage. In years subsequent to this mortgage payments will be greater and the owners will have less spare money to spend in the wider economy, and less ability to trade up the property ladder.
Is this storing up trouble for the future?
Source: Office of National Statistics, The Economist
The thing to remember is that even though early monthly payments are lower in a low interest rate/low inflation environment, the debt is still there and must be paid back. If house prices are also higher then the rungs of the property ladder have effectively moved further apart.
Simply put, in the absence of any shocks to the economy, those buying today are dedicating more their future earnings to servicing their debt than any other previous generation.
Lifetime affordability still counts.
Not many commentators, pundits, or pub experts really argue that housing is cheap. Many bears point to the real price of housing, or the price-earnings ratio and worry about a crash, whilst the more bullish point to the “affordability” and claim that we are not yet at an historic high.
However, it’s not often noted that the affordability description only focuses on the first year of payments and misses the point of higher payments in later years. Measuring the lifetime affordability of a mortgage might be more contentious, and may not affect purchase decisions, but it remains important, if not for its impact on house prices today then for the social and/or economic impacts tomorrow.
Whichever way you look at it there’s just no way around the fact that house prices are very, very expensive. High house prices alone do not mean that there will be a crash, but if there isn’t to be one there will have to be social consequences.
Part 2 -What’s less certain?
What’s less certain is why this has occurred, or what happens next. It’s clearly here that the bull vs. bear discussion really begins. There are quite a few arguments for either side, with the bears asserting that house prices will eventually (always next quarter) revert to some mean, whilst the bulls assert that house prices can continue to grow rapidly year on year forever with no consequences or risks… A quick summary of these arguments will form part 2 of this blog...
2) Housing - Why So Expensive?
Very few people argue that property is cheap today. By every measure, with the exception of first year “affordability”, housing costs more than ever before.
However, it is far from certain why this has occurred. Many press articles and “expert” reports concentrate on one explanation or another. But it’s a complex and thorny issue and there are quite a few arguments for either side. It is here that the bear-bull discussion gets more heated, with the “bears” generally using various arguments to assert that house prices are too high and will eventually (always next quarter) revert to some historical mean, whilst the bulls gather arguments that assert that it’s different this time and house prices are fair, and can continue to grow rapidly year on year forever with no risks and no consequences…
So why are houses so expensive? There are many theories, but generally they can be broken down into a few themes:
- Low interest rates
- Supply vs. demand
- Expanding money supply and the Global system
- Financial innovation
- Speculation and a psychology led market
Low Interest Rates
Unfortunately it is not that clear cut. The first confusion comes from a lack of general understanding regarding nominal vs. real interest rates. There is a fundamental difference. Nominal interest rates are those that are quoted by the press and generally known, whilst real interest rates account for inflation and are of real significance.
Looking at the graph of nominal interest rates below it can be seen that the house price booms of the 1970s and late 1980s actually occurred during times of high nominal interest rates. Futhermore there has never been a study that has found a link between nominal interest rates and any long-run determination in house prices.
 Source: Andrew Farlow
Source: Andrew FarlowReal interest rates take into account the inflation rate, and thus measure how the loan actually feels to repay. A 20% nominal rate with 50% inflation would feel very easy to pay after a few years, as your income would be freely growing by more than the debt costs you, but a 10% nominal rate at 0% inflation remains hard to pay, as your wages wouldn’t be increasing in the same way. In the first case the real interest rate is -30%, whilst in the second it is +10%.
If you look at the graph of real rates below you can see that real interest rates during the house price inflation of the late 1990s and early 2000s do not differ significantly from the preceding period, and are significantly higher the 1970s (a time of negative real interest rates - and when the concept of the housing ladder was born).
 Source: Farlow
Source: Farlow So throughout the 1990s real interest rates were similar and thus debt was no more affordable… But of course this is discussing the rational, real, cost of a mortgage over its entire lifetime. What lower nominal rates can do is increase the initial monthly affordability of the payments, and thus give the appearance of a cheaper mortgage. However, as outlined in part one, this is an illusion. All that really happens is that the payments for the mortgage are pushed further back into the lifetime of the loan, flattening the payment “pain” curve. Thus, whilst lower interest rates can be described as a facilitator for higher house prices, they are not a rational nor sensible driver, and we may be storing up problems for the future.
It also seems very unlikely that interest rates were the sole driver, as even nominal rates dropped long before the upturn in house prices, and prices continued to rise even though nominal interest rates rose by 35% in 2004, and again in 2006.
 Source: BBC News
Source: BBC NewsSupply
The supply scenario was highlighted by the UK government’s 2004 Barker report, which detailed a chronic failure of UK housing supply. In the late 1960s over 400,000 houses were built each year in the UK. Whilst in 2002 only 183,000 houses were built, of which 138,000 were built in England. Yet household formation in England is expected to increase by between 155,000 and 179,000 per year, and ran at an estimated 196,000 households per year from 1990 – 2000. This is clearly a problem.

Source: Barker Report
The Barker report went on to stress that to achieve a real annual house price trend increase of 1.8% an additional 70,000 private sector houses are required each year. Alternatively, to reach the EU average of a 1.1% real price increase per year then an extra 120,000 houses are needed each year - nearly double current output…
Demand
The Barker report also notes that the average size of UK households has been falling for some time, and that this results in some of the demand pressure.
It's worth noting that much of the figures that the Barker report was based upon were from government statistics and the 2001 national census. Thus they miss what has recently been quoted as being another major potential drive in house price demand: immigration.
Migration Watch UK predict that 2 million people will arrive in the UK every 10 years for the foreseeable future, and that the average immigration rate between 1998 and 2004 was around 166,000 per year. Some higher estimates put eastern European migration at over 500,000 per year since a number of states, most notably Poland, joined the EU in 2004. This could obviously lead to increased demand, and due to the nature of immigration this demand is likely to be heavily regionalised, with many migrants settling in the south east of England.


Source: BBC News
However, whilst supply vs. demand is often quoted as a key an issue in the UK, and at face value the figures seem stark, the control that supply vs. demand has over the full magnitude of recent house price inflation remains contentious.
This is particularly true within economic academia. Whilst a limited supply is noted, many economic modellers are unable to match the predicted consequences of this under-supply with the rapid and significant price increases experienced in the late 1990s and early 2000s. Furthermore, the undersupply has been relatively constant, yet price increases vary in rate significantly. The economic modelling of Muellbaur and Murphy, a pair of academics from Oxford University, suggest that the supply shortage of today (~0.25% of total dwellings) should push up real house prices by just 0.5% per year. That’s clearly a big disconnect from what has really happened, although the model does make many assumptions, not least requiring perfectly rational and fully informed consumers. But if the model is in anyway close to correct then there must be other variables that matter too.
Many argue that changes in family size and the trend to smaller household formation is an additional factor for housing demand. But the key point is that it is just that - a trend. It has been happening since the 1960s and as such is a gradual feature that has long existed in the market. Gradual societal changes are not clear explanations for the recent significant and rapid gain in house prices. The only recent step-change event that has occurred recently is the expansion of the EU in 2004, and the significant immigration experienced by the UK in subsequent years. Yet prices have been rising rapidly since the mid 1990s, with the rate of increase actually lowering from 2004.
There is one final point that casts doubt on the simple supply-demand driver: house prices have been rising globally. From the US, to Australia, Belgium, France, New Zealand, South Africa, Ireland, to Spain and others. Nearly every major economy (and many developing ones) have experienced a huge inflation in the price of property.
Expanding Money Supply and the Global System
Money supply is simply a measure of all the money (hard cash, loan debt, and saving accounts for example) in an economy. The total money supply can be expanded or contracted by central banks, such as the Federal Reserve or the Bank of England. This control over money is in practice a combination of setting interest rates, banking reserve ratios, and the purchase or sale of government securities, which are basically just an interest charging IOU from the government.
In an expanding monetary system the purchase of government securities releases funds to private banks that can then be loaned on to customers through fractional reserve banking (where the banks only have to keep a small percentage of their liabilities in reserve). Thus money from the central bank effectively multiplies as it moves through the banking system. Similarly a decrease in the central bank interest rate can make it more attractive to borrow (and loan on) monies. Effectively, the central banks “print” money.
In classic economic theory, if the supply of money is expanded too quickly then it will cause inflation, as there is more money chasing the same amount of goods.
One theory is that the rapid house price increases of the late 1990s and 2000s are the consequence of a more rapidly expanding money supply, as central banks effectively printed money in an effort to prevent worldwide recession and deflation, and an increasingly globalised economy kept interest rates at historic lows.
In the late 1990s many policy makers and economic commentators were worried about the dramatic entrance of two billion Chinese and Indian workers into a rapidly globalising worldwide economy. As these combined with falling commodity prices, falling bond yields, and falling producer prices economists began to fear that this would cause serious deflation, a terrible outcome for western economies that were heavily dependent on debt, and that had witnessed the decline and fall of Japan’s once triumphant economy.
 Source: The Economist
Source: The Economist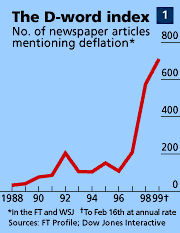
Source: The Economist
At the time of these worries the dot-com boom was in full growth and western economies were still growing. Indeed, the US Federal Reserve was actually raising rates. However on March the 10th 2000 the NASDAQ hit a high of 5,048 and the tech bubble burst, with the rapid fall continuing until 2003. As a result the major central banks worried about a major recession that would deliver the spectre of major deflation, so they rapidly eased monetary policy to encourage growth (and thus encourage inflation rather than deflation). This process was compounded by the 2001 terrorist attacks, when both the ECB and Fed dropped rates by ½ a percent. All in all, in an effort to prevent the imminent recession becoming a global collapse the Fed dropped interest rates eleven times by the end of the year, from 6.5% to just below 2%. The Federal Reserve, as central bank to the world’s reserve currency, led the way and other banks followed.

The increased money supply was further facilitated by the rise of China and other developing economies on the international foreign markets. Globalisation meant that US and western consumers could buy cheaply manufactured goods from China, driving the feared of deflationary pressures. Determined to keep its economy growing China pegged its exchange rate at a low level against the dollar, stabilising its access to its most important export market. Increasing foreign trade and rapid growth then provided the Chinese government with a huge trade surplus and a flood of foreign exchange. China has consistently re-invested this primarily in US bonds, enabling the US Federal Reserve to keep interest rates lower than they would have otherwise done. The strong demand for government bonds means that China has basically been increasing their price and lowering their yield. The effects of this are two fold. One is that the purchase of the bonds at higher prices effectively adds to the money supply, and the second is that their decreased yield means that other investors are forced to chase higher returns elsewhere. Whilst this effect is American-centric, where the Federal Reserve and the dollar lead, the world follows.
The theory is that a rapidly increasing money supply flooded the market with cheap credit, enabling exuberant house purchasers and investors to “afford” ever higher prices. Additionally, those stung by the stock market busts at the turn of the century distrusted the markets, preferring to invest in bricks and mortar than pensions and funds. Furthermore, institutional investors chasing ever decreasing yields in traditional markets looked at other potential avenues of investment and revenue creation.
However, the difficulty with assuming expanding money supply was the sole driver for house prices is that whilst the rate of house price increase did accelerate at this time, house prices had been rising in the UK since 1995. This rapid monetary easing cannot thus be held account for the entire boom, although it is likely to have been a major factor to its continuation, along with a closely related theme…
… Financial Innovation
The earliest of these can probably be credited to Lewis Ranieri, a college dropout. His key creations were Mortgage Backed Securities and Collateralised Mortgage Obligations. Simply put, these are a financial process that, for instance, converts the future revenues owed to a mortgage company by a suite of home loans into interest earning bonds that can be sold on to investors anywhere in the world.
This culture of rapid financial innovation continued throughout the 1990s, by which time J. P. Morgan and Merrill Lynch were marketing credit derivatives. The most common credit derivative is the credit default swap (CDS). A CDS is basically a financial vehicle that enables a bank or company to package up a stream of future revenues and further transfer the risk of the future revenues failing. For instance, a mortgage issuing company can package up a suite of mortgages into a Mortgage Backed Security and sell this to a second company. The second company can then manage its risk by issuing a further “interest” bearing credit derivative. This would earn the purchaser, a third company, an income, but at the risk of being forced to pay out to the issuer if the mortgage payers could no longer meet their obligations and the revenue stream of the Mortgage Backed Security failed.
This suite of complex financial products enables much wider trading and hedging of credit risk, facilitating companies to spread their risk according to their appetite – the mortgage issuers or MBS buyers can minimise their risks, whilst companies with an appetite for more risk can access a revenue stream. Additionally it allows the debts and derivatives to be recorded as assets on many companies books, and thus effectively removes institutional barriers to lending, as banks can draw on essentially unlimited funds to loan.
It is difficult to put a precise figure on how much this has affected the housing market. It is clear that this spread of risk had the effect of reducing the wariness of the mortgage issuing companies. The interest rate premium above the central bank rate lowered and application/vetting procedures eased. In general, whilst the market is very opaque and poorly understood, it can be safely said that the derivatives market markedly reduced the perception of risk across the entire industry. When combined with a loosening monetary policy and a pre-existing growth market it ensured that a flood of money entered the property industry chasing a piece of the action in the search for yield.
At the same time that financial innovation was removing barriers to money entering the housing market, regulatory change was providing a direction for the money to flow in the UK. In 1988 the UK’s Housing Act abolished security of tenure for tenants. In the late 1990s Buy to Let mortgages caught up with the legislation and became available to conventional borrowers (because of advanced risk management). Additionally, Mortgage Equity Withdrawal loans enabled those sitting on large paper wealth to access it. This enriched those already in property, and the money was either spent in the debt-led consumer boom, or it was invested, which leads to …

Source: Housepricecrash.com

Source: Housepricecrash.co.uk
… Speculation and Psychology
A final explanation for house price inflation is pure and simple speculation. Every expanding market has always attracted speculators and the housing market is no different. It has been suggested that the current market is strongly led by money pouring into it simply because it has grown so well over recent years. Participants don’t necessarily look at fundamentals, just that as the market continues to grow, or even accelerate, investors will pile in and prices will rise further and further. Some are investing in heavily geared Buy-to-Let properties, where the rental yield doesn’t cover the debt payments. Others simply leave the house empty, planning on selling at a later date. In the UK it is certainly clear that property market has become about more than just providing a roof over one’s head, and the percentage of Buy to Let investors has rocketed since the late 1990s. Commentators suggest that they have taken the role at the bottom of the market that used to be occupied by First Time Buyers, who now make up a much smaller percentage of the market than the historical norm.
The house price feeding frenzy has been further exacerbated by past rewards (an entire generation of owners have seen their wealth increase massively), and the resulting shift in press and television media attention. This has driven house prices to be regular front page news, and increases heralded as a boon for the economy. Furthermore, there is now an entire generation that has never experienced a major recession. Common sentiment is that house prices should be as high as they are, and that they are a good thing. Speculation and Psychology combine.


However, as with all of the suggested drivers behind the market, it is unlikely that speculation alone has driven the entire magnitude of house price inflation. It is likely simply a contributing factor.
Conclusion
All in all it can only be a fabrication to ascribe the significant house price rises of recent years to a single driving variable. Press reports, for the sake of readability, drastically over-simplify reality. There are likely to be many factors that are critical, and the relative influence of each is likely to have varied through time.
- House prices are at an all time REAL high, and the low inflation environment means that the real lifetime cost of the mortgage debt is also at a REAL high. Low interest rates do not have a fundamental affect on this, but low nominal rates do give the appearance of more affordable mortgages, encouraging consumers who have learnt only to measure cost only on an initial monthly basis.
- Supply and demand is clearly an issue in the UK, but doesn’t explain the global reach of house price inflation, nor its recent rapid and significant rise (immigration is a possible factor, but doesn’t tie well with the history)
- A loose monetary policy likely increased the money flowing into an already growing market, kicking off greater rises and triggering increased speculation.
- At the same time financial innovation reduced the financial industry’s traditional aversion to risk and enabled mortgage banks to meet the ever growing demand…
In a sense it's the perfect storm. But is it sustainable? What can we say about the future? And if nothing changes, what are the implications?
